课程信息

平台自	课程发表时间	分类	原始作者	原始地址	原始资源创建时间	原始资源更新时间
BiliBili	2024-08-26	视频	云凌Sapphire	【基础概念课】20分钟搞定「命题与量词」的基本概念与题目｜轻松上手｜排除坑点	2023-06-27	2023-06-27
BiliBili	2024-08-27	视频	云凌Sapphire	【基础概念课】20分钟搞定「逻辑与充分必要条件」的基本概念与题目｜轻松上手｜排除坑点	2023-06-27	2023-06-27

命题与量词

字数

2026 字

阅读时间

9 分钟

命题

• 概念：
  • 能判断真假的陈述句叫做命题，使用自然语言、符号、数学式表达，通常用小写英文字幕代表某个命题，若判断为真则为真命题，若判断为假则为假命题。
• 否定：
  • 对命题 $p$ 加以否定可得到新命题 $\mathrm{\neg }p$ (非$p$，$p$的否定)。[#非($ neg$\text{)](\#非(}$%20neg$))

量词

对存在未知变量而无法判断的陈述句（也就不是命题）添加量词对变量的取值范围进行限定以使该陈述句成为命题。

全称量词与全称命题

全称量词：在陈述中表示所述事务的全体，用符号 $\mathrm{\forall }$ 表示，语言“任意”、“所有”、“每一个”通常表示此意。

全称量词命题：含有全称量词的命题，形如“对集合 $M$ 中的所有元素$x,r(x)$”的命题，可简记为$\mathrm{\forall }x\in M,r(x)$ 。

存在量词与存在命题

存在量词：在陈述中表示所述事务的个体或部分，用符号 $\mathrm{\exists }$ 表示，语言“存在”、“有”、“至少有o个”通常属于此类

存在量词命题：含有存在量词的命题，形如“对集合 $M$ 中的所有元素$x,r(x)$”的命题，可简记为$\mathrm{\exists }x\in M,r(x)$。

否定或证明全称量词与存在量词

证明一个全称量词命题 $\mathrm{\forall }x\in A,p(x)$ 需要证明 $A$ 中所有元素 $x$ 都符合命题（即 $p(x)$ 成立）。

证明一个存在量词命题 $\mathrm{\exists }x\in A,q(x)$ 需要找到 $A$ 中一个元素 $x$ 符合命题（即 $q(x)$ 成立）。

否定一个全称量词命题 $\mathrm{\forall }x\in A,p(x)$ 需要找到 $A$ 中一个元素 $x$ 不符合命题（即 $p(x)$ 不成立）（也就是使其否定形式 $\mathrm{\exists }x\in A,\mathrm{\neg }p(x)$ 成立）。。

否定一个存在量词命题 $\mathrm{\exists }x\in A,q(x)$ 需要证明 $A$ 中所有元素 $x$ 都不符合命题（即 $q(x)$ 不成立）（也就是使其否定形式 $\mathrm{\forall }x\in A,\mathrm{\neg }q(x)$ 成立）。。

解题技巧

我们要证明一个量词成立或不成立时时：

| 情况 | 方法 | | --- | --- | | 全称 $\mathrm{\forall }$ | 举反例 | | 存在 $\mathrm{\exists }$ | 举成立 |

白	黑
大于	不大于/小于等于
小于	不小于/大于等于
等于	不等于
是	不是
都是	都不是
会	不会
至少有一个	一个也没有
至多有一个	至少有两个
都不是	至少有一个是

命题四形式

命题“若$p$，则$q$”由条件$p$与结论$q$组成，逆命题即将$p$与$q$换位，否命题即将$p$与$q$换质，由此可构成：

1. 原命题：若$p$，则$q$；
2. 逆命题：若$q$，则$p$；
3. 否命题：若非$p$，则非$q$；
4. 逆否命题：若非$q$，则非$p$.

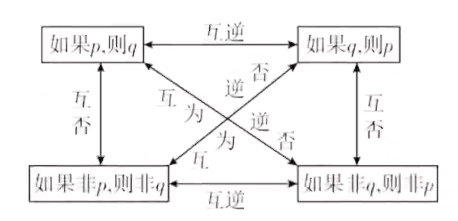
技巧

原命题与其逆否命题满足同真同假的关系 即：如果原命题为真，其逆否命题也为真；如果原命题为假，其逆否命题也为假。

[!example] 测试 写出命题“若$\mathrm{\neg }p$，则$q$”的逆否命题 Proofs： 逆：若$q$，则$\mathrm{\neg }p$ 逆否：若$\mathrm{\neg }q$，则$p$Answer：若$\mathrm{\neg }q$，则$p$

逻辑联结词：且(与)、或、非(否定)

使用逻辑联结词联结命题$p$与命题$q$，可得到一个新命题

注意

此处会使用主命题、分命题表示这些命题间的关系，这种表述是不规范的

且($\wedge$)

联结命题 $p$ 与 $q$ 可得到 $p\wedge q$ ( $p$ 且 $q$ ).

我们可以根据“且”的含义，将”且“用于定义集合的交集：$A\cap B=\{x\mid (x\in A)\wedge (x\in B)\}$

命题 $p\wedge q$ 的真假

$p$\ $p\wedge q$ \ $q$	真	假
真	真	假
假	假	假

观察上表可知，“主命题” $p\wedge q$ 中只要存在其中一个”分命题“为假就可判断出该“主命题”为假（一假即假）.

或($\vee$)

联结命题 $p$ 与 $q$ 可得到 $p\wedge q$ ( $p$ 或 $q$ ).

我们可以根据“或”的含义，将”或“用于定义集合的交集：$A\cup B=\{x\mid (x\in A)\vee (x\in B)\}$

命题 $p\vee q$ 的真假

$p$\ $p\vee q$ \ $q$	真	假
真	真	真
假	真	假

观察上表可知，“主命题” $p\vee q$ 中只要存在其中一个”分命题“为真就可判断出该“主命题”为真（一真即真）.

非($\mathrm{\neg }$)

"非"对应语言中"不是"、"全盘否定"、"问题的反面".

对命题 $p$ 加以否定可得到新命题 $\mathrm{\neg }p$ (非$p$，$p$的否定).

命题 $\mathrm{\neg }p$ 的真假

$\mathrm{\neg }p$ 与 $p$ 不能均为真或均为假，其互为否定.

即若 $p$ 为真，则 $\mathrm{\neg }p$ 为假；即若 $p$ 为假，则 $\mathrm{\neg }p$ 为真.

[!quote] 简单命题与复合命题 不含逻辑连词的命题称为简单命题;含逻辑联结词的命题称为复合命题.

如果对这方面感兴趣，或许可以看看逻辑

充要条件

充分条件与必要条件

NOTE

这是一个比较难理解的地方,故先在前面放一个图形以便于理解: $\mathrm{条}\mathrm{件}(p)\underset{\mathrm{必}\mathrm{要}\mathrm{性}}{\overset{\stackrel{\mathrm{充}\mathrm{分}\mathrm{性}}{\rightharpoonup }}{\leftharpoondown }}\mathrm{结}\mathrm{果}(q)$

[!example] 示例

• 中国人(条件;小范围)是亚洲人(结果;大范围)
• 知道别人家具体门牌号同时知道别人家的小区,只知道别人家的小区不能推导出具体门牌号

小范围可推导出大范围,但大范围不能推导出小范围

当有一个命题"如果 $p$ 则 $q$ "且该命题为真命题时，我们可以得到 $p\Rightarrow q$ ( $p$ 推出 $q$ ).此时称 $p$ 是 $q$ 的充分条件， $q$ 是 $p$ 的必要条件.

充要条件

若 $p\Rightarrow q$ ,且 $q\Rightarrow p$ 称 $p$ 是 $q$ 的充分且必要条件,简称 $p$ 是 $q$ 的充要条件( $q$ 当且仅当 $p$ ; $p$ 与 $q$ 等价)，记作 $p\iff q$ .

$p$ 与 $q$ 之间的四种关系与相应结论

$p$ 与 $q$ 的关系	结论
$p\Rightarrow q$ 但 $q\nRightarrow p$	$p$ 是 $q$ 的充分不必要条件 $q$ 是 $p$ 的必要不充分条件
$p\nRightarrow q$ 但 $q\Rightarrow p$	$p$ 是 $q$ 的必要不充分条件 $q$ 是 $p$ 的充分不必要条件
$p\Rightarrow q$ 且 $q\Rightarrow p$	$p$ 与 $q$ 互为充要条件
$p\nRightarrow q$ 且 $q\nRightarrow p$	$p$ 与 $q$ 互为既不充分也不必要条件

[!example] 测试 1.俗话说"便宜没好货",这句话中:"好货"是"不便宜"的( )

A. 充分条件

B. 必要条件

C. 充要条件

D. 既不充分也不必要条件

Answer:A

2.古语有言"不破楼兰终不还",这句话中:"破楼兰"是"还"的( )

A. 充分条件

B. 必要条件

C. 充要条件

D. 既不充分也不必要条件

Answer:B

贡献者

Kesager

文件历史

最后编辑于 11 个月前查看完整历史

05327-一股脑地提交pull